From how to why: An overview of causal inference in machine learning

Ravi Pandya

Artificial intelligence is good at predicting outcomes, but how do we go one step further? Here, we discuss how AI can use causal inference and machine learning to measure the effects of multiple variables – and why it’s important for technological progression.

In a major operator’s network control center complaints are flooding in. The network is down across a large US city; calls are getting dropped and critical infrastructure is slow to respond. Pulling up the system’s event history, the manager sees that new 5G towers were installed in the affected area today.

Did installing those towers cause the outage, or was it merely a coincidence? In circumstances such as these, being able to answer this question accurately is crucial for Ericsson.

Most machine learning-based data science focuses on predicting outcomes, not understanding causality. However, some of the biggest names in the field agree it’s important to start incorporating causality into our AI and machine learning systems.

——————————————————————————————-

Read the Ericsson white paper:  Artificial intelligence and machine learning in next-generation systems

——————————————————————————————-

Yoshua Bengio, one of the world’s most highly recognized AI experts, explained in a recent Wired interview: “It’s a big thing to integrate [causality] into AI. Current approaches to machine learning assume that the trained AI system will be applied on the same kind of data as the training data. In real life it is often not the case.”

Yann LeCun, a recent Turing Award winner, shares the same view, tweeting: “Lots of people in ML/DL [deep learning] know that causal inference is an important way to improve generalization.”

Causal inference and machine learning can address one of the biggest problems facing machine learning today — that a lot of real-world data is not generated in the same way as the data that we use to train AI models. This means that machine learning models often aren’t robust enough to handle changes in the input data type, and can’t always generalize well. By contrast, causal inference explicitly overcomes this problem by considering what might have happened when faced with a lack of information. Ultimately, this means we can utilize causal inference to make our ML models more robust and generalizable.

What exactly is causal inference?

When humans rationalize the world, we often think in terms of cause and effect — if we understand why something happened, we can change our behavior to improve future outcomes. Causal inference is a statistical tool that enables our AI and machine learning algorithms to reason in similar ways.

Let’s say we’re looking at data from a network of servers. We’re interested in understanding how changes in our network settings affect latency, so we use causal inference to proactively choose our settings based on this knowledge.

Inferring causes via randomized controlled trials

The gold standard for inferring causal effects is randomized controlled trials (RCTs) or A/B tests. In RCTs, we can split a population of individuals into two groups: treatment and control, administering treatment to one group and nothing (or a placebo) to the other and measuring the outcome of both groups. Assuming that the treatment and control groups aren’t too dissimilar, we can infer whether the treatment was effective based on the difference in outcome between the two groups.

However, we can’t always run such experiments. Flooding half of our servers with lots of requests might be a great way to find out how response time is affected, but if they’re mission-critical servers, we can’t go around performing DDOS attacks on them. Instead, we rely on observational data—studying the differences between servers that naturally get a lot of requests and those with very few requests.

What can we do with purely observational data?

There are many ways of answering this question. One of the most popular approaches is Judea Pearl’s technique for using to statistics to make causal inferences. In this approach, we’d take a  model or graph that includes measurable variables that can affect one another, as shown below.

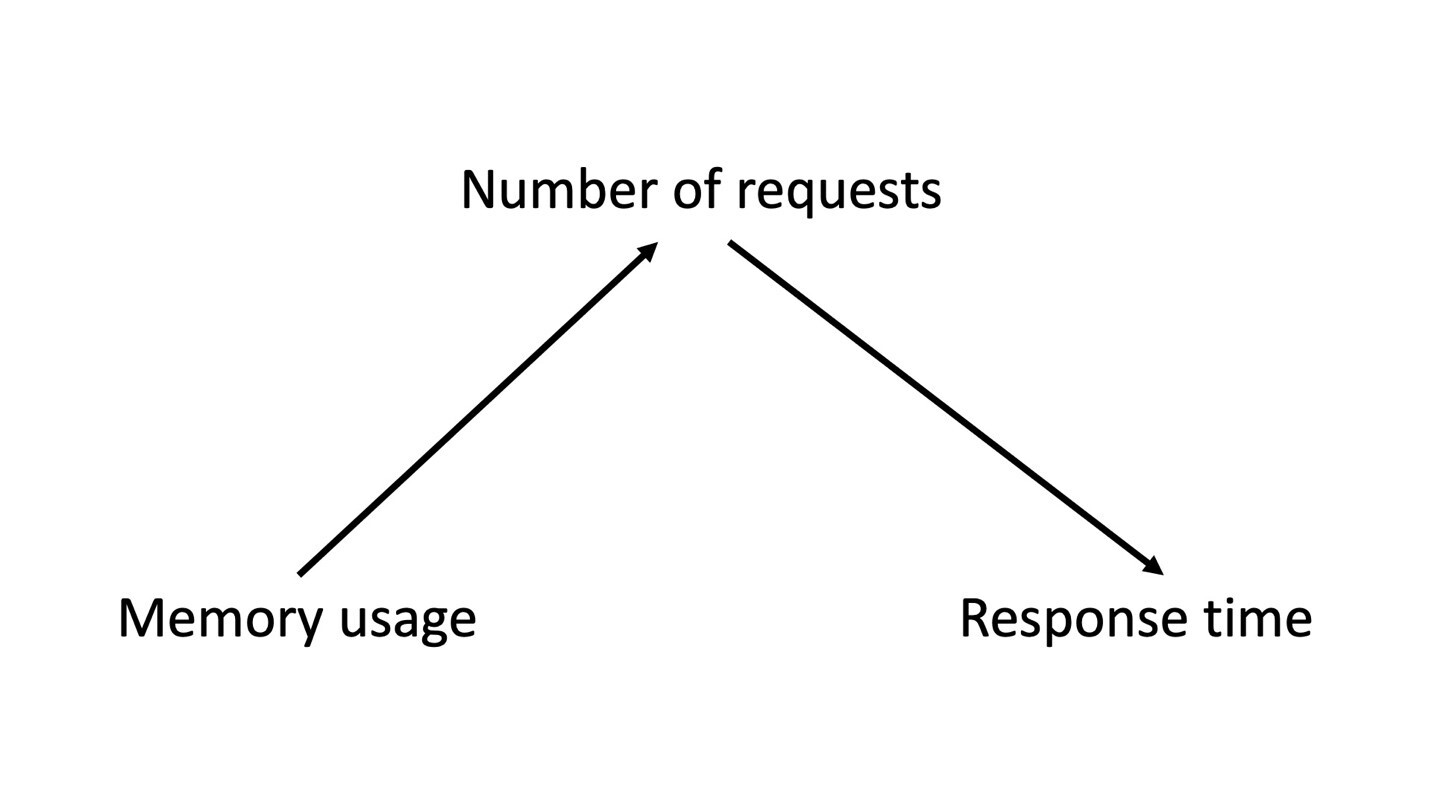
To use this graph, we must assume the Causal Markov Condition. Formally, it says that subject to the set of all its direct causes, a node is independent of all the variables which are not direct causes or direct effects of that node. Simply put, it is the assumption that this graph captures all the real relationships between the variables.

Another popular method for inferring causes from observational data is Donald Rubin’s potential outcomes framework. This method does not explicitly rely on a causal graph, but still assumes a lot about the data, for example, that there are no additional causes besides the ones we are considering.

Causal inference on an example server network

For simplicity, our data contains three variables: a treatment , an outcome , and a covariate . We want to know if having a high number of server requests affects the response time of a server.

• Treatment x is a binary variable (in all techniques presented here, this has to be true): 0 indicates a low number of server requests and 1 indicates a high number of requests
• Outcome y (in general it can be continuous, meaning it can take any value): the response time of the server (in seconds)
• Covariate z is another variable that could affect the outcome—here we consider the percentage of used memory on the server

In our example, the number of server requests is determined by the memory value: a higher memory usage means the server is less likely to get fed requests. More precisely, the probability of having a high number of requests is equal to 1 minus the memory value (i.e. P(x=1)=1-z , where P(x=1)  is the probability that x is equal to 1). The response time of our system is determined by the equation (or hypothetical model):

y=1⋅x+5⋅z+ϵ

Where ϵ is the error, that is, the deviation from the expected value of y given values of x and z depends on other factors not included in the model. Our goal is to understand the effect of x on y via observations of the memory value, number of requests, and response times of a number of servers with no access to this equation.

The average treatment effect

There are two possible assignments (treatment and control) and an outcome. Given a random group of subjects and a treatment, each subject  has a pair of potential outcomes:  and , the outcomes Y_i (0) and Y_i (1) under control and treatment respectively. However, only one outcome is observed for each subject, the outcome under the actual treatment received: Y_i=x⋅Y_i (1)+(1-x)⋅Y<_i (0). The opposite potential outcome is unobserved for each subject and is therefore referred to as a counterfactual.

For each subject, the effect of treatment is defined to be Y_i (1)-Y_i (0) . The average treatment effect (ATE) is defined as the average difference in outcomes between the treatment and control groups:

E[Y_i (1)-Y_i (0)]

Here, E denotes an expectation over values of Y_i (1)-Y_i (0) for each subject , which is the average value across all subjects. In our network example, a correct estimate of the average treatment effect would lead us to the coefficient in front of x in equation (1) .

If we try to estimate this by directly subtracting the average response time of servers with x=0 from the average response time of our hypothetical servers with x=1, we get an estimate of the ATE as 0.177 . This happens because our treatment and control groups are not inherently directly comparable. In an RTC, we know that the two groups are similar because we chose them ourselves. When we have only observational data, the other variables (such as the memory value in our case) may affect whether or not one unit is placed in the treatment or control group. We need to account for this difference in the memory value between the treatment and control groups before estimating the ATE.

Inferring causes via propensity score matching

One way to correct this bias is to compare individual units in the treatment and control groups with similar covariates. In other words, we want to match subjects that are equally likely to receive treatment.

The propensity score e_i for subject i is defined as:

e_i=P(x=1∣z=z_i ),z_i∈[0,1]

or the probability that x is equal to 1—the unit receives treatment—given that we know its covariate z is equal to the value z_i. Creating matches based on the probability that a subject will receive treatment is called propensity score matching. To find the propensity score of a subject, we need to predict how likely the subject is to receive treatment based on their covariates.

The most common way to calculate propensity scores is through logistic regression:

1. Transform data into training data x and labels y , the columns of x being the covariates (in our example, x has one column with the memory usage), and  y as a binary vector of the actual treatment received for each subject i.e. whether the number of requests is high or not (the outcome variable is ignored)
2. Train a logistic regression model on x with labels y
3. Use the trained model to predict the probability of y=1  for the training data x; we are predicting how likely the server is to get a lot of requests given how much of its memory was used
4. The predicted probabilities are the propensity scores

Now that we have calculated propensity scores for each subject, we can do basic matching on the propensity score and calculate the ATE exactly as before. Running propensity score matching on the example network data gets us an estimate of 1.008 !

What does the estimate tell us?

We were interested in understanding the causal effect of binary treatment x variable on outcome y . If we find that the ATE is positive, this means an increase in x results in an increase in y. Similarly, a negative ATE says that an increase in x will result in a decrease in y .

This could help us understand the root cause of an issue or build more robust machine learning models. Causal inference gives us tools to understand what it means for some variables to affect others. In the future, we could use causal inference models to address a wider scope of problems — both in and out of telecommunications — so that our models of the world become more intelligent.

Special thanks to the other team members of GAIA working on causality analysis: Wenting Sun, Nikita Butakov, Paul Mclachlan, Fuyu Zou, Chenhua Shi, Lule Yu and Sheyda Kiani Mehr.

If you’re interested in advancing this field with us, join our worldwide team of data scientists and AI specialists at GAIA.

Read more

In this Wired article, Turing Award winner Yoshua Bengio shares why deep learning must begin to understand the why before it can replicate true human intelligence.

In this technical overview of causal inference in statistics, find out what’s needed to evolve AI from traditional statistical analysis to causal analysis of multivariate data.

This journal essay from 1999 offers an introduction to the Causal Markov Condition.

References

1. https://www.ericsson.com/en/blog/2020/2/causal-inference-machine-learning