Which Patients are in Greater Need: A counterfactual analysis with reflections on COVID-19

Scott Mueller and Judea Pearl

We are pleased to introduce the writing of Professor Judea Pearl, UCLA, World Leader in AIWS Award and a Mentor of AIWS.net:

I feel an obligation to share with you a couple of ideas on how AI can offer new insights and new technologies to help in pandemic situations like the one we are facing.

I describe them briefly below, with the hope that you can discuss them further with colleagues, students, and health-care agencies, whenever opportunities avail themselves.

1. Data Fusion
   ————–

Much has been said about how ill-prepared our health-care system was/is to cope with catastrophic outbreaks like COVID-19. The ill-preparedness, however, was also a failure of information technology to keep track of and interpret the vast amount of data that have arrived from multiple heterogeneous sources, corrupted by noise and omission, some by sloppy collection and some by deliberate misreporting. AI is in a unique position to equip society with intelligent data-interpreting technology to cope with such situations.

Speaking from my narrow corner of causal inference research, a solid theoretical underpinning of this data fusion problem has been developed in the past decade (summarized in this PNAS paper https://ucla.in/2Jc1kdD), and is waiting to be operationalized by practicing professionals and information management organizations.

2. Personalized care and counterfactual analysis
   ————–

Much of current health-care methods and procedures are guided by population data, obtained from controlled or observational studies. However, the task of going from these data to the level of individual behavior requires counterfactual logic, such as the one formalized and “algorithmitized” by AI researchers in the past three decades.

One area where this development can assist the COVID-19 efforts concerns the question of prioritizing patients who are in “greatest need” for treatment, testing, or other scarce resources. “Need” is a counterfactual notion (i.e., invoking iff conditionals) that cannot be captured by statistical methods alone. A recently posted blog page https://ucla.in/39Ey8sU demonstrates in vivid colors how counterfactual analysis handles this prioritization problem.

Going beyond priority assignment, we should keep in mind that the entire enterprise known as “personalized medicine” and, more generally, any enterprise requiring inference from populations to individuals, rests on counterfactual analysis. AI now holds the most advanced tools for operationalizing this analysis.

Let us add these two methodological capabilities to the ones discussed in the virtual conference on “COVID-19 and AI.” AI should prepare society to cope with the next information tsunami.

Best wishes,

Judea

 

With COVID-19 among us, our thoughts naturally lead to people in greatest need of treatment (or test) and the scarcity of hospital beds and equipment necessary to treat those people. What does “in greatest need” mean? This is a counterfactual notion. People who are most in need have the highest probability of both survival if treated and death if not treated. This is materially different from the probability of survival if treated. The people who will survive if treated include those who would survive even if untreated. We want to focus treatment on people who need treatment the most, not the people who will survive regardless of treatment.

Imagine that a treatment for COVID-19 affects men and women differently. Two patients arrive in your emergency room testing positive for COVID-19, a man and a woman. Which patient is most in need of this treatment? That depends of course on the data we have about men and women.

A Randomized Controlled Trial (RCT) is conducted for men, and another one for women. It turns out that men recover $57\%$ of the time when treated and only $37\%$ of the time when not treated. Women, on the other hand, recover $55\%$ of the time when treated and $45\%$ of the time when not treated. We might be tempted to conclude that, since the treatment is more effective among men than women, $20\%$ compared to $10\%$, that men benefit more from the treatment and, therefore, when resources are limited, men are in greater need for those resources than women. But things are not that simple.

Let us examine the data for men and ask what it tells us about the number that truly benefit from the treatment. It turns out that the data can be interpreted in a variety of ways. In one extreme model, the $20\%$ difference between the treated and untreated amounts to saving the lives of $20\%$ of the patients who would have died otherwise. In the second extreme model, the treatment actually saved the lives of all $57\%$ of those who recovered, and killed the other $37\%$ who died; they would have recovered otherwise, as did the $37\%$ recoveries in the control group. Thus the percentage of men saved by the treatment could be anywhere between $20\%$ and $57\%$, quite a sizable range.

Applying the same reasoning to the women’s data we find an even wider range. In the first model, $10\%$ out of $55\%$ recoveries were saved by the treatment and $45\%$ would recover anyhow. In the second extreme model, all $55\%$ of the treated recoveries were saved by the treatment while $45\%$ were killed by it.

Summarizing, for men, the percentage of beneficiaries may be anywhere from $20\%$ to $57\%$, while for women, anywhere from $10\%$ to $55\%$. It should start to be clear now why it’s not so clear that the treatment cures more men than women. Looking at the two intervals in figure 1 below, it is quite possible that as much as $55\%$ of the women and only $20\%$ of the men would actually benefit from the treatment.

Figure 1: Percentage of beneficiaries for men vs women

One might be tempted to argue that men are still in greater need because the guarantee for curing a man is higher than that of a woman ($20\%$ vs $10\%$), but that argument would neglect the other possibilities in the spectrum. For example, the possibility that exactly $20\%$ of men benefit from the treatment and exactly $55\%$ of women benefit, which would reverse our naive conclusion that men should be preferred.

Such coincidences may appear unlikely at first glance but we will show below that it can occur and, more remarkably, that we can determine when they occur given additional data. But first let us display the extent to which RCTs can lead us astray.

Below is an interactive plot that displays the range of possibilities for every RCT finding. It uses the following nomenclature. Let $Y$ represent the outcome variable, with $y=\text{recovery}$ and $y’=\text{death}$, and $X$ represent the treatment variable, with $x=\text{treated}$ and $x’=\text{not treated}$. We denote by y_xyx​ the event of recovery for a treated individual and by y_{x’}yx’​ the event of recovery for an untreated individual. Similarly, y’_xy’x​ and y’_{x’}y’x’​ represent the event of death for a treated and an untreated individual, respectively.

Going now to probabilities under experimental conditions, let us denote by P(y_x)P(yx​) the probability of recovery for an individual in the experimental treatment arm and by P(y’_{x’})P(y’x’​) the probability of death for an individual in the control (placebo) arm. “In need” or “cure” stands for the conjunction of the two events y_xyx​ and y’_{x’}y’x’​, namely, recovery upon treatment and death under no treatment. Accordingly, the probability of benefiting from treatment is equal to P(y_x, y’_{x’})P(yx​,y’x’​), i.e., the probability that an individual will recover if treated and die if not treated. This quantity is also known as the probability of necessity and sufficiency, denoted PNS in (Tian and Pearl, 2000) since the joint event (y_x, y’_{x’})(yx​,y’x’​) describes a treatment that is both necessary and sufficient for recovery. Another way of writing this quantity is P(y_x > y_{x’})P(yx​>yx’​).

We are now ready to visualize these probabilities:

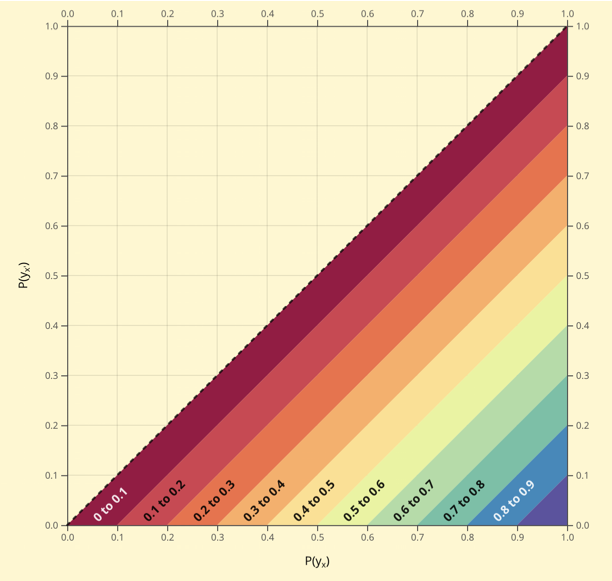
Let’s first see what the RCT findings above tell us about PNS — the probability that the treatment benefited men and women. Click the checkbox, “Display data when hovering”. For men, $57\%$ recovered under treatment and $37\%$ recovered under no treatment, so hover your mouse or touch the screen where P(y_x)P(yx​) is $0.57$ and P(y_{x’})P(yx’​) is $0.37$. The popup bubble will display 0.2 \leqslant P(y_x > y_{x’}) \leqslant 0.570.2⩽P(yx​>yx’​)⩽0.57. This means the probability of the treatment curing or benefiting men is between $20\%$ and $57\%$, matching our discussion above. Tracing women’s probabilities similarly yields the probability of the treatment curing or benefiting women is between $10\%$ and $55\%$.

We still can’t determine who is in more need of treatment, the male patient or the female patient, and naturally, we may ask whether the uncertainty in the PNS of the two groups can somehow be reduced by additional data. Remarkably, the answer is positive, if we could also observe patients’ responses under non-experimental conditions, that is, when they are given free choice on whether to undergo treatment or not. The reason why data taken under uncontrolled conditions can provide counterfactual information about individual behavior is discussed in (Pearl, 2009, Section 9.3.4). At this point we will simply display the extent to which the added data narrows the uncertainties about PNS.

Let’s assume we observe that men choose treatment $40\%$ of the time and men never recover when they choose treatment or when they choose no treatment (men make poor choices). Click the “Observational data” checkbox and move the sliders for $P(x)$, $P(y|x)$, and $P(y|x’)$ to $0.4$, $0$, and $0$, respectively. Now when hovering or touching the location where P(y_x)P(yx​) is $0.57$ and P(y_{x’})P(yx’​) is $0.37$ yields 0.57 \leqslant P(y_x > y_{x’}) \leqslant 0.570.57⩽P(yx​>yx’​)⩽0.57 in the popup bubble. This tells us that exactly $57\%$ of men will benefit from treatment.

We can also get exact results about women. Let’s assume that women choose treatment $45\%$ of the time, and that they recover $100\%$ of the time when they choose treatment (women make excellent choices when choosing treatment), and never recover when they choose no treatment (women make poor choices when choosing no treatment). This time move the sliders for $P(x)$, $P(y|x)$, and $P(y|x’)$ to $0.45$, $1$, and $0$, respectively. Clicking on the “Benefit” radio button and tracing where P(y_x)P(yx​) is $0.55$ and P(y_{x’})P(yx’​) is $0.45$ yields the probability that women benefit from treatment as exactly $10\%$.

We now know for sure that a man has a $57\%$ chance of benefiting compared to $10\%$ for women.

The display permits us to visualize the resultant (ranges of) PNS for any combination of controlled and uncontrolled data. The former characterized by the two parameters P(y_x)P(yx​) and P(y_{x’})P(yx’​) and the latter by the three parameters $P(x)$, $P(y|x)$, and $P(y|x’)$. Note that, in our example, different data from observational studies could have reversed our conclusion by proving that women are more likely to benefit from treatment than men. For example, if men made excellent choices when choosing treatment ($P(y|x)=1$) and women made poor choices when choosing treatment ($P(y|x)=0$). In this case, men would have a $20\%$ chance of benefiting compared to $55\%$ for women.

But even when PNS is known precisely, one may still argue that the chance of benefiting is not the only parameter we should consider in allocating hospital beds. The chance for harming a patient should be considered too. We can determine what percentage of people will be harmed by the treatment by clicking the “Harm” radio button at the top. This time the popup bubble will show bounds for P(y_x < y_{x’})P(yx​<yx’​). This is the probability of harm. For our example data on men ($P(x)=0.4$, $P(y|x)=0$, and $P(y|x’)=0$), trace the position where P(y_x)P(yx​) is $0.57$ and P(y_{x’})P(yx’​) is $0.37$. You’ll see that exactly $37\%$ of men will be harmed by the treatment. Next, we can use our example data on women, $P(x)=0.4$, $P(y|x)=0$, $P(y|x’)=0$, P(y_x) = 0.55P(yx​)=0.55, and P(y_{x’}) = 0.45P(yx’​)=0.45. The probability that women are harmed by treatment is, thankfully, $0\%$.

What do we do now? We have a conflict between benefit and harm considerations. One solution is to quantify the benefit to society for each cured person versus each killed person. Let’s say the benefit to society to treat someone who will be cured if and only if treated is $1$ unit. However, the harm to society to treat someone who will die if and only if treated is $2$ units. This is because we lost the opportunity to treat someone who would benefit from treatment, we killed someone, and we incurred a loss of trust from this poor decision. Now, the benefit of treatment for men is $1\cdot 0.57–2\cdot 0.37=-0.17$ and the benefit of treatment for women is $1\cdot 0.1–2\cdot 0=0.1$. If you were a policy-maker, you would prioritize treating women. Treating men actually yields a negative benefit on society!

The above demonstrates how a decision about who is in greatest need, when based on correct counterfactual analysis, can reverse traditional decisions based solely on controlled experiments. The latter, dubbed A/B in the literature, estimates the efficacy of a treatment averaged over an entire population while the former unravels individual behavior as well. The problem of prioritizing patients for treatment demands knowledge of individual behavior under both treatment and non-treatment and must therefore invoke counterfactual analysis. A complete analysis of counterfactual-based optimization of unit selection is presented in (Li and Pearl, 2019).

References

1. Ang Li and Judea Pearl. Unit selection based on counterfactual logic. Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pages 1793–1799, 2019.
2. Judea Pearl. Causality. Cambridge University Press, 2009.
3. Jin Tian and Judea Pearl. Probabilities of causation: Bounds and identification. Annals of Mathematics and Artificial Intelligence, 28:287–313, 2000.