Causal vs. Statistical Inference

Why is correlation not enough, or is correlation enough? The question bugging the scientific community for a century. A machine learning view on the subject.

Causal inference, or the problem of causality in general, has received a lot of attention in recent years. The question is simple, is correlation enough for inference? I am going to state the following, the more informed uninformed person is going to pose a certain argument that looks like this:

Causation is nothing else than really strong correlation

I hate to break it to you if this is your opinion, but no it is not, it is most certainly not. I can see that it is relatively easy to get convinced that it is, but once we start thinking about it a bit we are easily going to come to the realization that it is not. If you are still convinced otherwise after reading this article, please contact me for further discussion because I would be interested in your line of thought.

For illustrating the point that correlation doesn´t necessarily mean causation, let us take a look at the simplest formula of correlation, or rather the famous Pearson correlation coefficient:

So this correlation coefficient is in the range from -1 to 1, telling us if the variables are negatively or positively correlated. In other words, when one is over its mean and the other one is over or under its mean at the same time, respectively. This correlation coefficient is named after the famous mathematician Karl Pearson, to whom we owe a great deal. People argue that he is the founder of modern statistics, he also introduced the first university statistics department in the world at University College London. Thank you, professor Pearson. But there is one thing he was not really keen on, and that is the argument of causality.

Notice that there is a problem straight away with the correlation formula, which is that there is no sense of direction. Although two variables can be highly correlated with each other, we don’t really know what caused what. To give you an example, take the weather. If it is raining, you most certainly have clouds. Naturally, you ask yourself the question, what caused the rain. Take the correlation between rain and clouds, you notice that there is a positive correlation. Nice, but so what? Can you really say that the clouds caused the rain and not the rain caused the clouds? No, you cannot, not based on this simple correlation coefficient. Perhaps you would notice though one thing, obviously, the clouds appear before the rain. Then you would realize, but wait, if I introduce a temporal aspect to my variables and calculate something as lagged correlation, then I should realize that the clouds cause rain and not the other way around. This is true, but this brings me to my next argument.

The problem of chocolate addicted Nobel prize winners

There is one famous study that showed that there is a strong correlation between a country’s chocolate consumption and the number of Nobel prize winners coming from this country. So would you say that chocolate consumption causes one’s probability to become a Nobel prize winner to be higher and start consuming chocolate like crazy immediately? I hope not, I suspect that it is reasonable to expect that chocolate does not cause one to be a Nobel prize winner. So let us extract two variables from this statement. B— Being a Nobel prize winner, A— consuming chocolate. The causal diagram for this statement would basically look like this:

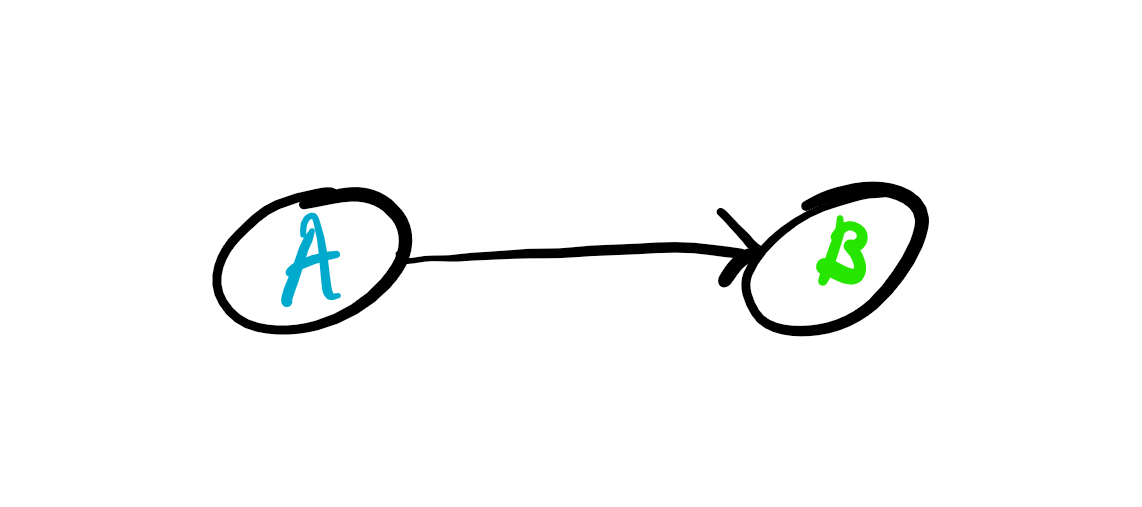
The arrow meaning that A causes B. As you can see, this is a very primitive causal diagram. Now we can come to the point, although we have strong correlation between chocolate consumption and Nobel prize winning, we can ask ourselves, is there some other variable, C, such as the country’s wealth that causes both Nobel prize winning and chocolate consumption, or is it the country’s educational system that causes both and so on. Let us imagine, as indeed is the case, that there is a common cause C for both. Then the causal diagram looks like this:

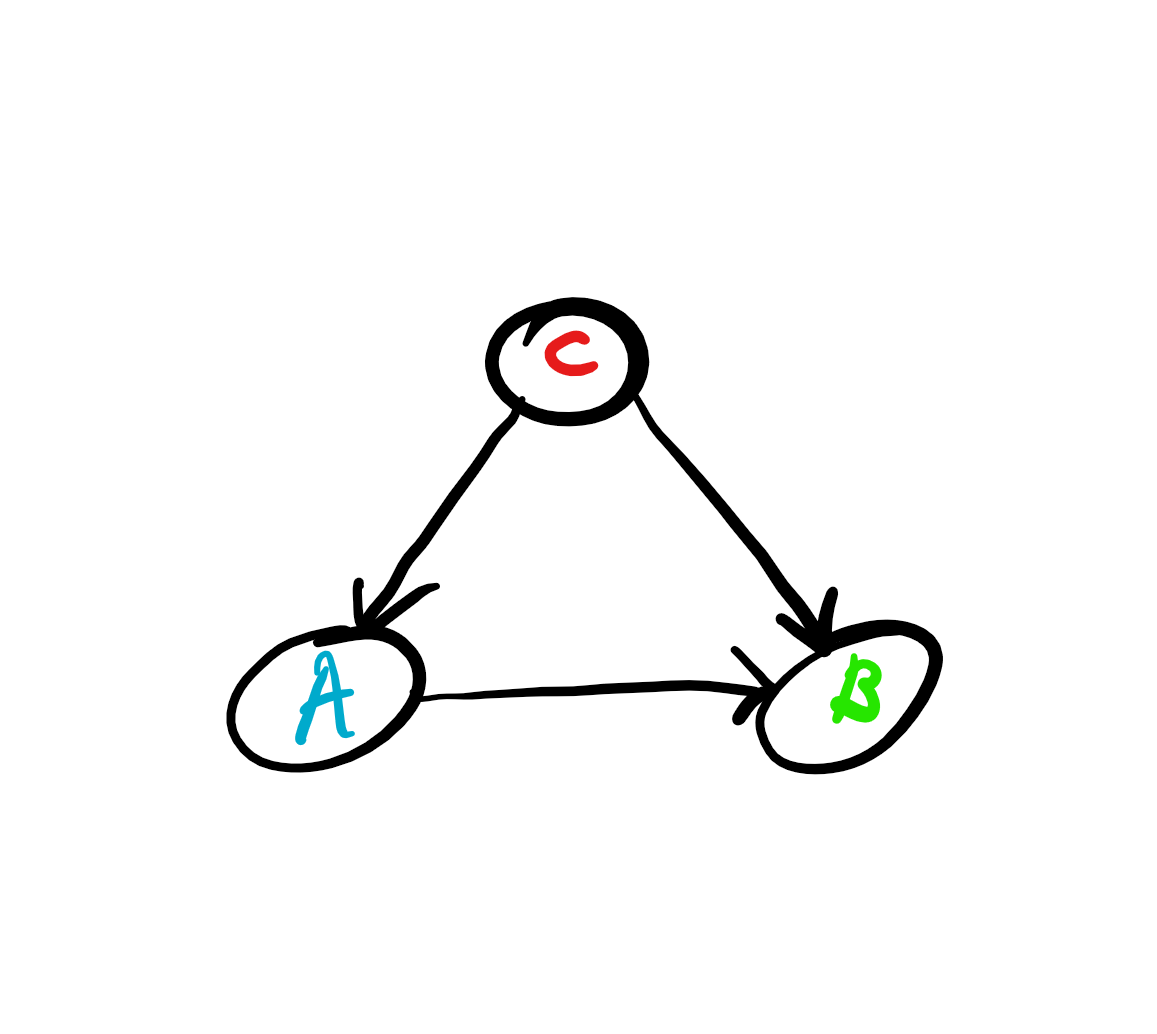
Now we can mention Reichenbach’s common cause principle which states that if variables A and B have a common cause, C, then when we condition on C, the correlation between these variables is wiped out, meaning that the conditional distributions of the random variables conditioning on the common cause become independent. Nice enough. So actually the causal diagram that we should be looking at is the following:

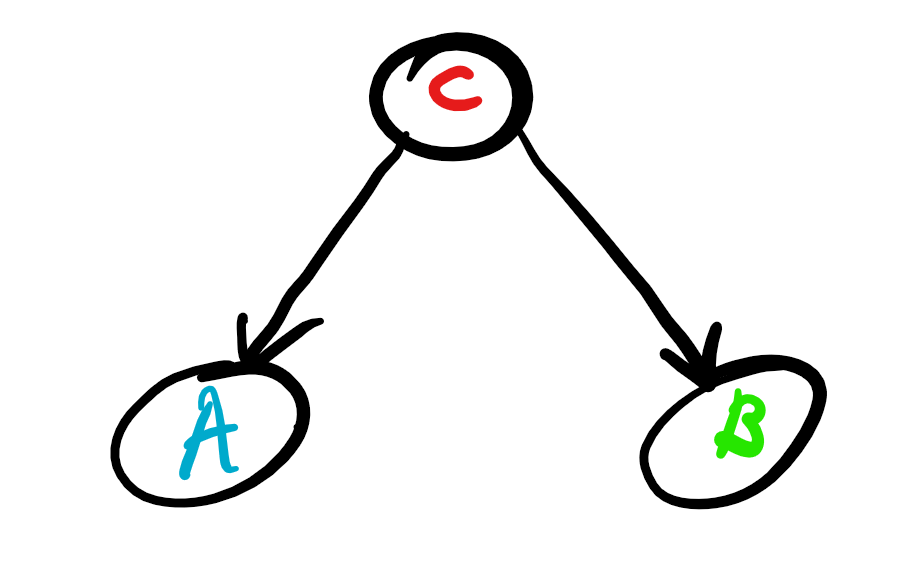
This is what causality is all about, establishing that there is not a common cause that makes A and B look like as if A causes B. This practice has well been established though in the medical community in the form of medical trials, well before people started talking about causal inference. So how do we establish this? Firstly, we are going to call a medical trial with a more general, useful name. We are going to call it a controlled experiment. Controlled experiments are nice, we can act upon a variable directly and see how our other variables change in our causal diagram. In a medical trial, this would be taking groups of people 1 and 2, 1 group 1 taking the placebo and group 2 taking the actual medicine to the sickness and observing the results. Naturally, in medical trials we want these people to come from the same distribution, i.e. to be similar. Actually, ideally we want them to be the same, this would be the perfect medical trial that would eliminate any other potential common causes, but this is unrealistic to expect, a perfect controlled experiment. Now you observe the results of the groups and determine based on some confidence if the medicine is efficient in curing the disease.

In causal language, this is called an intervention. If we can take a variable and set it manually to a value, without changing anything else. This is basically stating we take the same people before we applied the placebo and the medicine and then apply both, to see if the disease has been cured by the medicine or something else. Generally, people find it difficult to differentiate between intervention and setting a probability of an event’s realization to 1. The difference is that intervention results in two different causal diagrams on which we can calculate our probabilities and reach a conclusion about the actual causal structure of the diagram.

Luckily, we have Prof. Judea Pearl to thank for inventing causal calculus, for which he has received the prestigious Turing award and will probably be known further on as the founder of modern causal inference. I would suggest reading his books on causality for diving more deeply into the topic:

1. The Book of Why

2. Causality: Models, Reasoning and Inference

3. Causal Inference in Statistics: A Primer

I personally think that the first one is good for a general audience since it also gives a good glimpse into the history of statistics and causality and then goes a bit more into the theory behind causal inference.

Till now we were talking about a bit of statistics but the question remains how does this actually reflect on AI algorithms, that is, machine learning algorithms. The connection is rather straight forward. The current approaches that we use cannot distinguish cause from effect by learning from the data since we are mostly talking about probability distributions in machine learning and learning models that basically see things occur at the same time and automatically assume that one is predictive of the other. Personally, I cannot imagine that these models can or will be deployed safely in the real world. Especially in the case if we want to develop something as Schmidhueber’s artificial scientist, we need to be able to distinguish between cause and effect and reason about them.

In science, we constantly need to accept or reject hypotheses to reach conclusions. This is why causal inference is not just good to have, it is a necessity if we want to reach valid conclusions. There are countless examples where studies have been made that resulted in false conclusions as a consequence of not being able to use statistics properly, as shown in this article or this. I am confident that the field is going to cause a scientific renaissance in the community. As a takeaway from this article, remember the following which you hopefully already know:

Correlation does not imply causation

Till next time!

Source https://towardsdatascience.com/causal-vs-statistical-inference-3f2c3e617220