Causal inference without graphs

In a recent posting on this blog, Elias and Bryant described how graphical methods can help decide if a pseudo-randomized variable, Z, qualifies as an instrumental variable, namely, if it satisfies the exogeneity and exclusion requirements associated with the definition of an instrument. In this note, I aim to describe how inferences of this type can be performed without graphs, using the language of potential outcome. This description should give students of causality an objective comparison of graph-less vs. graph-based inferences. See my exchange with Guido Imbens [here].

Every problem of causal inference must commence with a set of untestable, theoretical assumptions that the modeler is prepared to defend on scientific grounds. In structural modeling, these assumptions are encoded in a causal graph through missing arrows and missing latent variables. Graphless methods encode these same assumptions symbolically, using two types of statements:

1. Exclusion restrictions, and
2. Conditional independencies among observable and potential outcomes.

For example, consider the causal Markov chain 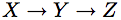 which represents the structural equations:

with 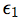 and 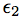 being omitted factors such that X, 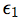,  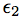are mutually independent.

These same assumptions can also be encoded in the language of counterfactuals, as follows:

(3) represents the missing arrow from X to Z, and (4)-(6) convey the mutual independence of X, 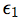, and .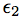
[Remark: General rules for translating graphical models to counterfactual notation are given in Pearl (2009, pp. 232-234).]

Assume now that we are given the four counterfactual statements (3)-(6) as a specification of a model; What machinery can we use to answer questions that typically come up in causal inference tasks? One such question is, for example, is the model testable? In other words, is there an empirical test conducted on the observed variables X, Y, and Z that could prove (3)-(6) wrong? We note that none of the four defining conditions (3)-(6) is testable in isolation, because each invokes an unmeasured counterfactual entity. On the other hand, the fact the equivalent graphical model advertises the conditional independence of X and Z given Y, X _||_ Z | Y, implies that the combination of all four counterfactual statements should yield this testable implication.

Another question often posed to causal inference is that of identifiability, for example, whether the
causal effect of X on Z is estimable from observational studies.

Whereas graphical models enjoy inferential tools such as d-separation and do-calculus, potential-outcome specifications can use the axioms of counterfactual logic (Galles and Pearl 1998, Halpern, 1998) to determine identification and testable implication. In a recent paper, I have combined the graphoid and counterfactual axioms to provide such symbolic machinery (link).

However, the aim of this note is not to teach potential outcome researchers how to derive the logical consequences of their assumptions but, rather, to give researchers the flavor of what these derivation entail, and the kind of problems the potential outcome specification presents vis a vis the graphical representation.

As most of us would agree, the chain 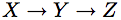 appears more friendly than the 4 equations in (3)-(6), and the reasons are both representational and inferential. On the representational side we note that it would take a person (even an expert in potential outcome) a pause or two to affirm that (3)-(6) indeed represent the chain process he/she has in mind. More specifically, it would take a pause or two to check if some condition is missing from the list, or whether one of the conditions listed is redundant (i.e., follows logically from the other three) or whether the set is consistent (i.e., no statement has its negation follows from the other three). These mental checks are immediate in the graphical representation; the first, because each link in the graph corresponds to a physical process in nature, and the last two because the graph is inherently consistent and non-redundant. As to the inferential part, using the graphoid+counterfactual axioms as inference rule is computationally intractable. These axioms are good for confirming a derivation if one is proposed, but not for finding a derivation when one is needed.

I believe that even a cursory attempt to answer research questions using (3)-(5) would convince the reader of the merits of the graphical representation. However, the reader of this blog is already biased, having been told that (3)-(5) is the potential-outcome equivalent of the chain X—>Y—>Z. A deeper appreciation can be reached by examining a new problem, specified in potential- outcome vocabulary, but without its graphical mirror.

Assume you are given the following statements as a specification.

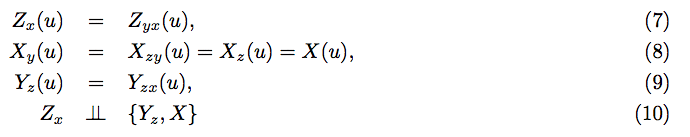
It represents a familiar model in causal analysis that has been throughly analyzed. To appreciate the power of graphs, the reader is invited to examine this representation above and to answer a few questions:

a) Is the process described familiar to you?
b) Which assumption are you willing to defend in your interpretation of the story.
c) Is the causal effect of X on Y identifiable?
d) Is the model testable?

I would be eager to hear from readers
1. if my comparison is fair.
2. which argument they find most convincing.

Source http://causality.cs.ucla.edu/blog/index.php/2014/11/09/causal-inference-without-graphs/